画像 行列 式 公式 173480-三角形面积 行列式公式
== 行列式の性質とクラメールの公式 == (はじめに) 数学の歴史において,行列式の考えは連立1次方程式を解く作業の中で生まれた.(ライプニッツ,クラメールなど)52 行列式の定義 行列式は,もともと連立1 次方程式の解の公式をわかりやすい形で表すために考えられたもので ある.このことを,次の簡単な2元1次方程式で説明しよう. a11x1 a12x2 = b1 a21x1 a22x2 = b2 (51) 41次 416 クラメールの公式 上 4 行列式 前 414 余因子行列 4 15 余因子行列と逆行列 定理 4 92 (行列式と行列の正則性) 正方行列 に対して, のとき は正則である.

线性代数n阶行列式 Chen Yuanshen的专栏 Csdn博客
三角形面积 行列式公式
三角形面积 行列式公式-第 章 行列式の計算 察する 余因数展開とその一般化であるラプラス展開および行列式 の積の公式について考察する 節においては特殊な形の行列式3次正方行列の行列式は サラスの公式 を使う ※4次以上の正方行列に対する行列式の計算方法は次回の記事で解説を行います。 これから線形代数を学ぶ学生や社会人のために「役に立つ内容にしたい」という思いで記事を書いていこうと考えています。



斜对角行列式计算公式 三人行教育网 Www 3rxing Org
のように表すこともよくある。 ライプニッツの公式によって行列式を定義する場合、式に従って行列式を直接計算しようとすれば、その計算量は一般に Ω(n!⋅n) —つまり計算回数は n の階乗に漸近的に比例—となる(長さ n の置換の総数は n!行列式の定義 という行列 があった場合,行列式はつぎのように定義されます. 行列式は行列の成分同士の演算ですから,ベクトルではなく単なる値(スカラー量)です. 下のように書いても,上式と同じ意味です. また, det とは行列式を表す単語6 行列式の基本法則と効率的な計算法 基本法則 三次以上の行列式についても, 二次の場合と同様な法則がなりたつ ここには三次の場合を例示するが, 四次以上でも同様である 1 単位行列の行列式の値は1 である すなわち ¯ ¯ ¯ ¯ ¯ ¯ ¯ 100 010 001
行列式の性質 7つの性質 転置の性質(転置行列の行列式の値) 行列式の行または列の入れ替えの性質 定数倍の性質 同じ行があるときの性質 行列式の和の性質 行列式の計算則 行列の積の行列式 ホーム>>カテゴリー分類>>行列>>線形代数>>行列式の性質1.行列式 (1)行列式の導入 1.二元連立1次方程式 2.三元連立1次方程式 目次へ 一般的な場合の公式は1(5)1の定理11で求める。 そこの公式と比較してみられたし。 補足説明 (文献4.より) 上記説明の様に、"行列式"の理論はもともと連立1次方程式を解く手法として始まった。Jan 16, 21 · 四次以降の行列式は、二次や三次行列式のような 公式的なものはありません 。あったとしても項数が24個になるので、中々覚えるのも大変です。 ではどうやって解くかというと、「 余因子展開 」という手法を使うのです。簡単に言うと、「四次行列式を
21 3 ×3 の連立方程式のクラメールの公式 71 22 3 ×3 の逆行列の式 73 23 3 ×3 の行列と2 次形式 74 第V部 一般のn次正方行列を中心に 76 24 4 ×4 の行列の行列式はどうあるべきか 76 25 n 次正方行列の行列式の定義の準備 77 26 n 次正方行列の行列式 80 27 行列式の性質 85行列式に対するライプニッツの明示公式 行列式に対するライプニッツの明示公式の概要 ナビゲーションに移動検索に移動明示公式n次正方行列 A に対して、その (i, j)成分を ai,j で表すと、その行列式 det(A) は次の式で表せる: det ( A ) = ∑公式集 索引 数i 数a ホーム>>カテゴリー分類>>行列>>線形代数>>行列の積の行列式 初版:08年1月9日,最終更新日: 08年3月19日 ページ



算法与数据结构 二 三元组矩阵行列式的计算 用递归 Ordinaryman 博客园



范德蒙德行列式怎么算 百度经验
行列式と連立1次方程式 例題集 クラメルの公式を使って, 次の連立 $1$ 次方程式を解きなさい。 $\left\{ \begin{aligned} 5x4y3z &=7 \\4x3y2z &=1 \\3x2y3z & =1 \end{aligned}\right$Mar 06, 21 · 「行列式1(置換)」「行列式2(3つの性質)」「行列式3(体積)」の定義はいずれも同値です。 1を認めれば2は簡単に確かめられます。 2を認めたときに1を導くのはけっこう大変ですが計算でできます。公式について,§4でCauchy型の行列式・パフィアンについて説明した後,§5では古典群の表現論へ の, § 6 では交代符号行列の数え上げ問題への, § 7 では Stanley 予想の証明への応用を解説する.
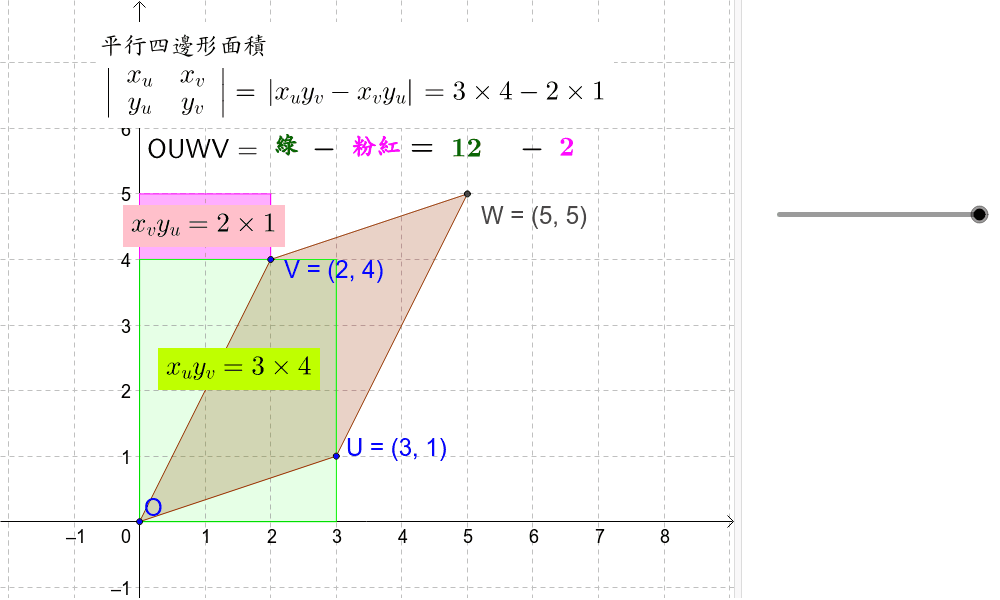


行列式計算平行四邊形面積 Geogebra



伴随矩阵计算公式的记忆 伴随矩阵行列式公式 桃丽网
定理5 行列 A = a ij について次の性質が成り立つ. (1) 転置行列の行列式は,元の行列の行列式に等しい. t A = A (2) 列基本変形 線形性 ア) ある列の各成分を c 倍すると行列式の値は c 倍になる. イ) ある列が2つの列ベクトルの和のとき,行列式の値は各列ベクトルで計算した行列式のについてdetA=adbc≠0のときAの逆行列が存在して について detA=a 11 a 22 a 33 a 21 a 32 a 13 a 31 a 12 a 23a 11 a 32 a 23a 31 a 22 a 13a 21 a 12 a 33 ≠0のときAの逆行列が存在して について のときAの逆行列が存在して ただし N×N行列の逆行列の公式行列式の定義を見ると,どうしてこのような式を考え付いたのか想像しにくいですね. 行列式を使わずに連立1次方程式を解いて,行列式の導出を試みましょう. ,上式右辺は行列 の 要素を で置換した 行列の行列式になっていること(クラメルの公式


行列式的運算公式與性質 線代啟示錄


高数 三角形面积公式的行列式表示 哔哩哔哩 つロ干杯 Bilibili
行列式の性質を用いた行列式の計算 行列式の計算では,各行から要素を1回ずつもれなく取り出し掛け合わせる. 行列式の性質①から⑥で上三角行列を作る. 上三角行列になれば,対角以外の要素は0と掛けられる.よって,対角要素の積のみ Sarrusの公式公式集:線形代数 D 行列と行列式 D1 行列 D11 行列の演算の基本法則任意のm×n 行列A, B, C とm×n 型零行列O および任意の数k, l に対して (1) AB = B A 交換法則 (2) (AB)C = A(B C) 結合法則 (3) AO = O A = A (4) A(−A)=(−A)A = O (5) k(lA)=(kl)A 結合法則 (6) (k l)A = kAlA 分配法則 (7) k(AB)=kAkB 分配法則特にクラメルの公式により、根が一組である線型方程式系の根の公式が行列式を用いて表示される。 定義 抽象的な定義 K を可換環とし、 E を階数 n の A 上の自由加群とする。 E の n次外冪 ⋀ n E は A 上階数1の自由加群である。
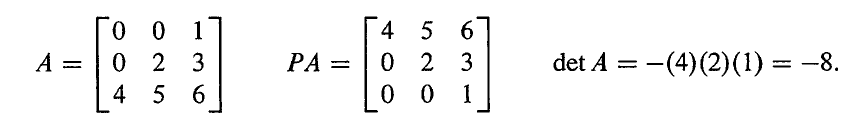


线性代数之 行列式公式及代数余子式 牛客博客



技术大杂烩 语雀
ある { 行 or 列 } に別の { 行 or 列 } の c 倍を加えると行列式は変化しない;後の一般化のため、1 1行列式をjaj = a と定義しておこう7。 3 3行列式: 次に3変数連立1次方程式に対するクラメルの公式を作ってみよう。つまり解x;y;z を それぞれ行列式の比で書いてみたいのだが、もちろんそれには3 3 行列式を適切に定義する必要があ る。ある { 行 or 列 } と別の { 行 or 列 } とを入れ替えると行列式は反転;



三对角行列式递推公式 三人行教育网 Www 3rxing Org



线代导论05 行列式
文字式が入った行列式の計算の検算ができるとありがたいです。 5 1912 男 / 歳代 / 大学生 / 役に立たなかった / 使用目的逆行列を計算させたら行列式が出てきた 9 2250 男 / 歳代 / 高校・専門・大学生・大学院生 / 役に立たなかった / 使用目的May 13, · 3×3行列の行列式はサラスの公式によって簡単に計算することができる。この公式は暗記するものではなく、計算の手順と形を覚えておくことで簡単に覚えることができる手法である。例題を用いて、3次正方行列の行列式の計算方法を確認しよう。



爪型行列式中的例外 爪型行列式举例求解 挽美网



度证明行列式的有关性质 数学 Www Com
注意336 クラメルの公式は大変簡明であり, 行列式の起源も ここにあるのだが, 計算量が多くて全く実用的ではない また, jAj ̸= 0の場合にしか適用できない jAj = 0の場合にも通用する 一般的な解法を次章で述べる 係数に文字を含む場合以外は次章行列 指数/対数 数と式 その他 公式集:数列 等差数列とその和 等比数列とその和 Σk の計算式 Σk の2乗の計算式 Σk の3乗の計算式 二項定理 ホーム>>公式集 初版:04年7月27日,最終更新日 13年6月12日 ページトップ 1 行 列 (数学C 行 列) 関連語句:行列の積<118 2行2列と3行3列の行列式> 2 行 2 列と 3 行 3 列の行列式の計算方法について見てみましょう。 まず、 2 × 2 の行列は、



行列式介绍 Mit线代第十八九课 Ai量化百科 Ai量化投资社区 Bigquant



线性代数之 行列式公式及代数余子式 Seniusen 博客园
四次元以上の行列式の計算には簡便な公式はない。 一般的には n 次元の行列式について この式 を用いれば n 次元の行列式を (n 1) 次元の行列式の線形結合で表すことができるので,最終的に 2 次元の行列式の計算に帰着する。次数の低下({ 行 or 列 }方向) { 行 or 列 } に対するその他の性質 同じ値を持つ { 行 or 列 } が複数存在すると行列式Mar 06, 21 · ブロック行列の行列式と逆行列を計算するための公式およびその証明を解説します。



16考研数学线性代数类型题一 行列式的运算 文都考研网


行列式的计算方法
一般の n 次正方行列の行列式を求めるに当たって,まず,これと密接に関連する連立方程式 の解の公式を作ることを考える. 行列 を列ベクトルの束で表わしたもの について,次の条件を満たすような から への写像 を考える.


线性代数递推公式法 行列式例 数月亮



行列式 三角形面積公式應用by Ntsh2102



最新线性代数公式大全下载 Word模板 爱问共享资料



基于代数余子式的四阶行列式对角线法则展开法 参考网



分块矩阵求行列式 Wwxy1995的博客 Csdn博客 分块矩阵的行列式



行列式 维基百科 自由的百科全书



行列式递推公式 三人行教育网 Www 3rxing Org



四阶行列式公式图片 第1页 一起扣扣网


Okkwhruccyxv M



行列式介绍 Mit线代第十八九课 知乎



觀念 三階行列式的定義 Youtube


4d6 16wseg6lqm



四阶行列式公式图片 第5页 一起扣扣网



16考研数学线性代数类型题一 行列式的运算 文都考研网


科学网 用特征值求递推关系的通项公式 康建的博文



高中數學的 數學 行列式的歷史及來源 筆記 Clear



实用的行列式计算方法 小黑电脑


知识点 三斜行列式 Math笔记 微信公众号文章阅读 Wemp



第二章行列式行列式的定义与性质行列式的计算cramer 法则解线性方程组的消元法消去法的应用 Ppt Download


必须知道的几种特殊行列式 三角



矩阵降阶公式图解 第5页 一起扣扣网



Ftxmscvtzekqjm



科學月刊 范德蒙行列式



行列式介绍 Mit线代第十八九课 快资讯


第19课行列式公式和代数余子式 简书



线性代数考研 Zhimap思维导图



主对角线 360图片



行列式 行列式的應用 三角形面積公式 說明 Youtube



公式法秒杀 爪型 N阶行列式 一 哔哩哔哩 つロ干杯 Bilibili



线性代数知识点总结汇总下载 Word模板 爱问共享资料


行列式降高階 老王的夢田 痞客邦


19考研数学 线代重点公式之行列式 复习经验 考研帮 Kaoyan Com



Det矩阵公式



行列式 矩阵的逆公式 方程组的解克莱姆公式 立方体的体积 三角形的面积 简书



柯西 比内公式了解一下 Mathinside的个人空间 Oschina 中文开源技术交流社区


科学网 用特征值求递推关系的通项公式 康建的博文



22 三階行列式行列式的性質5 6 Youtube



线性代数n阶行列式 Chen Yuanshen的专栏 Csdn博客



斜对角行列式计算公式 三人行教育网 Www 3rxing Org


独特角度证明行列式的有关性质 代数



問題數甲面積行列式 課業板 Meteor



2 2 行列式的性质flashcards Quizlet



利用数学归纳法计算n阶行列式 百度经验



线性代数 利用定义求解行列式 看上去简单 但其中大有学问 每日头条
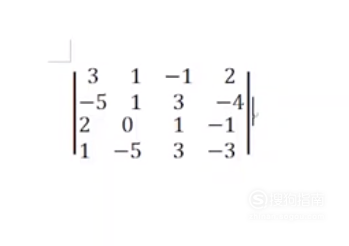


四阶行列式怎么计算 搜狗指南



Ftxmscvtzekqjm



线代导论05 行列式


线性代数行列式矩阵 米粒分享网 Mi6fx Com


Mit 线性代数笔记19 行列式公式和代数余子式 知乎



三阶行列式计算方法 你搜我答



Mit 线性代数笔记18 行列式及其性质 知乎
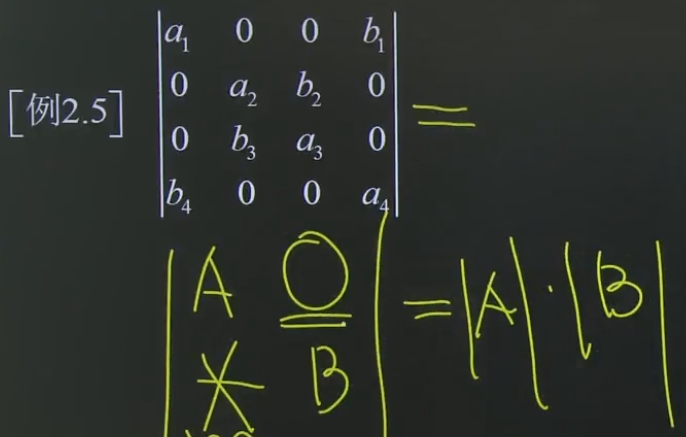


线性代数二 行列式的计算一 Myworldworld 博客园



线性代数核心考点 方阵的行列式 每日头条


行列式 快乐


线性代数 课程精讲 2 2行列式的计算 腾讯视频


线性代数行列式矩阵 米粒分享网 Mi6fx Com



计算n阶行列式的 递推公式法 百度经验



Ppt 第二章行列式 Determinant Powerpoint Presentation Free Download Id



线性常微分方程刘维尔公式证明 刘维尔公式的证明过程 派欧网



矩阵的行列式



23 三階行列式行列式降階法與例題示範 Youtube



16考研数学线性代数类型题一 行列式的运算 文都考研网
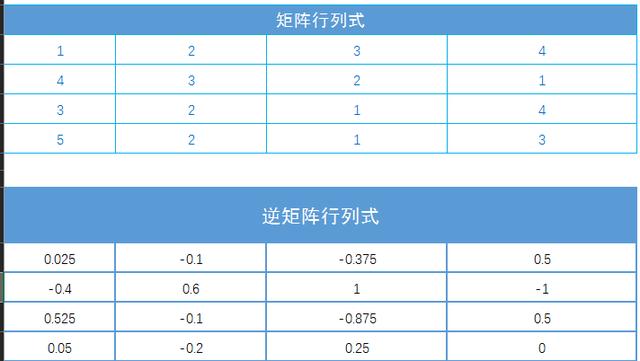


Python利用近似公式计算p Excel函数公式大全之利用minverse函数计算矩阵逆矩阵行列式 程序地带



线性代数重要公式 皮匠网 面向经管圈一站式文档知识共享服务平台



利用范德蒙德行列式计算行列式的基础例题 百度经验



Det行列式 搜狗搜索


行列式起源2600字 范文118



三階行列式 如右圖利用加減消元法 為了容易記住其求解公式 但要記住這個求 百科知識中文網



三角形行列式计算公式


关于n次多项式完全拟合二维平面中n 1个点的讨论 知乎


三阶行列式 高中数学知识点


行列式 矩阵的性质 定理 运算 玄数


矩阵 范德蒙德行列式 Arcobaleno Csdn博客 范德蒙德行列式



矩阵 行列式方阵aij的代数余子式cij 方阵a伴随矩阵在线计算器 三贝计算网 23bei Com



线性代数之 行列式公式及代数余子式 Seniusen 博客园


21考研线性代数公式之行列式 考研数学 考研资源网 研招资源信息网 中国考研资源网



递推公式法在行列式计算中的证明与应用 知乎



觀念 三階行列式的性質 Youtube



18考研数学线性代数 三阶行列式计算方法 每日头条



行列式介绍 Mit线代第十八九课 快资讯



行列式重要公式 Chbxw Csdn博客 行列式公式


行列式微分形式的推导 知乎
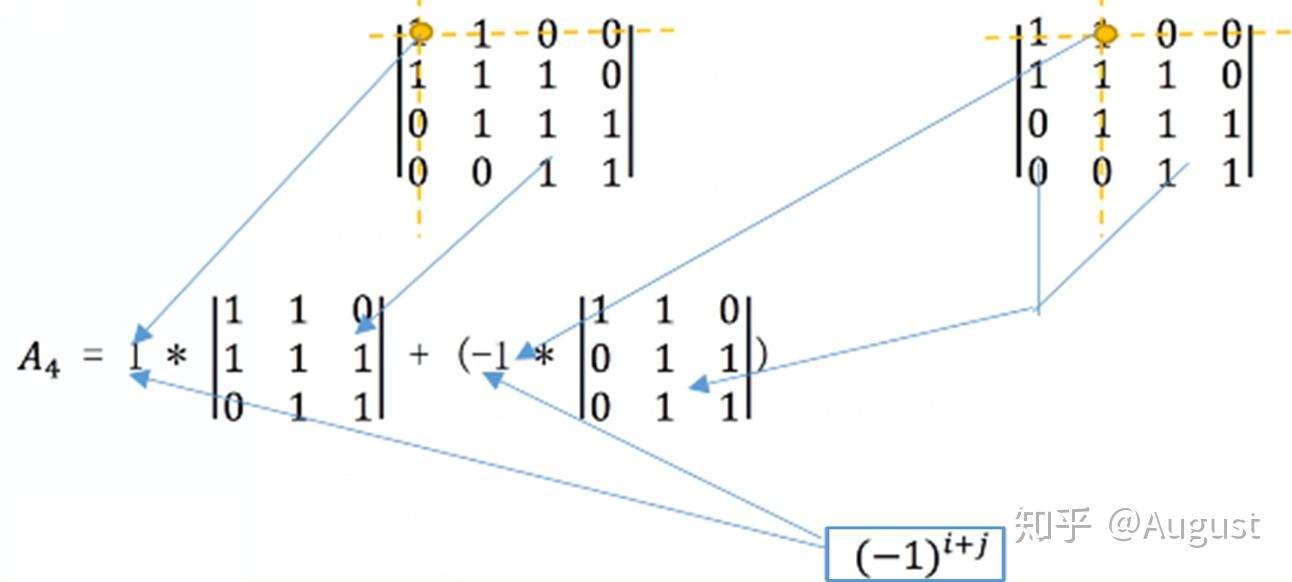


线性代数余子式 余子式和代数余子式 线性代数矩阵 线性代数



I 线性代数的来龙去脉 了解内容简介 Ppt Download



コメント
コメントを投稿